Ugo Bardi氏の『化石燃料: 私たちはセネカの崖の縁にいるのだろうか?』
本稿は、ローマ・クラブおよびASPO(association for the study of peak oil)のメンバーで、フィレンツェ大学地球科学学部の物理化学の教授であるUgo Bardi氏のブログRESOURCE CRISIS(旧Cassandra’s Legacy)2014年12月7日付けの記事"Fossil fuels: are we on the edge of the Seneca cliff? "を訳したものである。
私は以前、Ugo教授の『セネカ効果:衰退局面が成長局面よりも速いワケ』を紹介している。そこでは「汚染」の影響としてセネカ効果が示されたが、本稿では、新たな解釈として、生産ピーク付近での価格高騰がセネカ効果をもたらすことが示唆される。

「もしもあらゆるものが出来上がるのと同じくらいゆっくりと滅びるのであれば、それは私たちの弱さと私たちの住む世界にとって何らかの慰めとなったことだろう。だが、現実には成長の速度は遅く、破滅に至る時はすみやかだ。」 ルキウス・アンナエウス・セネカ、ルーキーリウスへの手紙、n. 91 (註:大柴芳弘訳『セネカ哲学全集6』(岩波書店)による)
このセネカの観察力は、原油のような非再生可能資源の生産など、多くの現代における事例にも当てはまるように思われる。はてな、私たちは「セネカの崖」の縁にいるのだろうか?
システムダイナミクスに取り組んでいる人々にはよく知られた教義がる。それは問題を悪くする解が数多あるというものだ。しばしば、人々は問題がどういうものなのかを完全に理解できると思っているようだが、同じくらいしばしば、人々は問題に対処して悪い方向に進むきらいがある。それは"pushing the lever in the wrong direction"のような言い回しで表される概念でもある。
化石燃料については、減耗問題があることを私たちは皆、理解しているが、これまでのところ、その解決策は、もっとたくさん、もっと深く掘削して、とにかく掘削し続けるということなのだ。そして、どんなに困難で金がかかろうと、すべての可能な源泉から燃料を絞り出すことで、過去数年間は在来油田の生産低下を埋め合わせて生産量の成長を保つことができた。だが、それは真の解決策なのだろうか?つまり、現在の成長のために将来、急速な減耗という代償を払うことになるのではないだろうか?
この疑問は、「セネカの崖」という言葉で言い表される。それは、非再生可能資源の生産が生産量のピークを過ぎた後にいかに急速に減退するかを示すために、2,3年前に私が提示した概念である。グラフを用いて示される振る舞いは下のようなものだ。
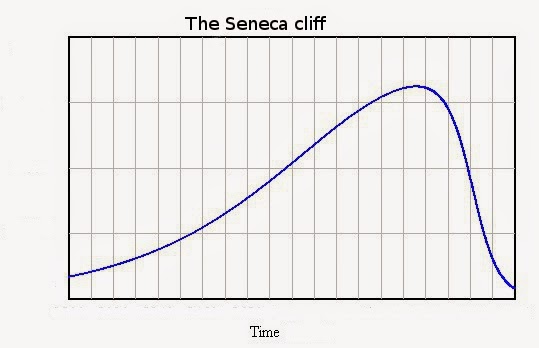
それは単なる理論モデルではない。ピークに達した後で資源の生産が崩壊したいくつかの歴史的事例が実在するのだ。たとえば、カスピ海のチョウザメに関するデータがあり、私が「ピーク・キャビア」と名付けた事例だ。
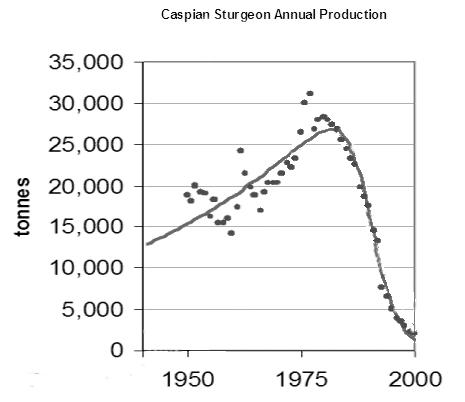
世界の石油および天然ガスの生産についてもこのような事態に直面する危険を私たちは冒しているのだろうか?私の見解では、イエスだ。類似点があるのだ。化石燃料もキャビアも代替不可能な資源である。どちらの場合も、ピークに達したときとその後、価格が急上昇した。そして、カスピ海のチョウザメが明瞭なセネカの崖を示したのならば、石油と天然ガスも同じことを示し得るだろう。ともあれ、いくらか詳細な内容に進もう。
私のセネカモデルの最初のバージョンでは、生産の急減は、汚染の拡大が生産システムへの加重負担となることで新規の資源開発に利用出来る資源量を減じさせることになるという観点から解釈された。しかしながら、私が(この度)発見したことは、セネカ型の挙動は汚染が増えるシステムではむしろ免れぬものながら、人々がシステムを「延命」しようして通常よりも急速に生産の拡大をシステムに強いるときにもいつでもセネカ型の挙動が現れるというものなのだ。
というのは、上記のカスピ海のチョウザメの場合については、汚染の拡大が(問題に寄与してきたかもしれないが)生産の急激な崩壊の原因になりそうもないのである。むしろ、崩壊の主要な要因は希少かつ代替不可能な資源(キャビア)の価格上昇の効果だったように思われる。高い価格が、できるだけ多くの魚を海から集めることにますます多くの資源を投資するように生産者を誘惑したからだ。しばらくは上手くいったが、つまるところ、存在しないチョウザメを捕ることは出来ない。やがて、大失敗となった。セネカの崖の古典的な事例だ。
この現象はモデル化可能だろうか?可能だ。後で、私はこの事例に関するモデルを詳述する。この考えのエッセンスは、生産者が生産量を保つためには新しい資源の開発に利益のある割合を再投資する必要があるという点にある。しかしながら、新しい投資の収率は時と共に減少してしまう。というのは、もっとも利益になる資源(例えば、油田)が最初に開発されるからだ。結果として、資本はますます新規投資に利用できなくなる。やがて生産量は最大値に達し、その後、減少する。企業が新たな資源に利益の一定割合を再投資すると仮定するならば、そのモデルは「ハバート曲線」として知られる対称的なベル型の曲線となる。
しかしながら、後で詳述するように、もしも高い価格が新規の生産のための開発に向けられる追加的な資本を与えることになるならば、減少過程が延期される。不幸にも、資本となる資源を速く燃やすことの対価として成長が達成されるわけだ。最終的な結果は、もはや対称的なハバート曲線ではなく、おなじみのセネカ型の曲線となる。減耗過程は成長過程よりも急激になる。
このことは、化石燃料について、私たちが直面していることなのだろうか?もちろん私たちは単に定性的なモデルを扱っているにすぎないのだが、他方では、定性的なモデルはしばしば堅固なものであり、たとえモデルが正確な時期の予想される出来事を私たちに教えてくれないとしても、予期されることについての様々な考えを私たちに与えてくれるものだ。目下進行中の原油価格の崩壊現象は新規油田の開発を維持するために必要な資本を欠乏しつつあることの徴候なのかもしれない。そうだとすると、私たちが言えることは、苦難が、とても酷い苦難が待っている、ということなのだ。おそらくセネカの崖は私たちの近未来の姿となるだろう。
____________________________________________________________________
利益から非再生可能資源の生産への割り当て分を増加させた結果としてのセネカ型曲線
ウーゴ・バルディ 2014年12月7日
注意:これは公式な科学論文ではない。これは、capex(補註:不動産等の価値や耐久年数を延ばすための経費)の割合を増加させると、非再生可能資源の生産にどんな影響を与え得るのかを示すために構想された、「封筒の裏」で行った粗っぽい計算だ。もっと洗練された公表に値する研究にするために私を手伝ってくれるなら、共同研究を歓迎するよ。
自由市場における非再生可能資源の開発を記述するシステムダイナミクス・モデルの基礎は、BardiとLavacchi による2009年の論文に詳述されている。その論文で展開されたモデルでは、非再生可能資源(R)は決まった量の初期ストック(埋蔵量)として存在することが仮定された。資源ストックは徐々に資本ストック(C)に変換されて、次いで、それが徐々に減耗することが仮定された。時間の関数として二つのストックの挙動は、2式の連立微分方程式によって記述される。
R’ = – k1*C*R
C’ = k2*C*R – k3*C
ここで、R’とC’は、時間の関数としてのストックのフローを表し(R’はいわゆる「生産量」である)、ksは定数である。これが「骨子」となるモデルなのだが、それでも「ベル型」のハバート曲線を再現でき、過去の事例に適用可能である。そして、このシステムに三つ目のストック(汚染)を加えれば、成長よりも速く減衰する、前のめりにゆがんだ生産曲線、すなわち「セネカ曲線」が現れる。
二つのストックからなるシステム(つまり、汚染を考慮しない)もまた、上記の方程式に修正をほどこすならば、セネカ曲線を生じ得る。特に、次のように記述し得る。
R’ = – k1*k3*C*R
C’ = ko*k2*C*R – (k3+k4)*C.
ここで、k3は生産に再投資された資本割合を明示しており、一方、k4は資本の低下(あるいは何らかの非生産的利用)に関わる比例係数である。このとき、生産量は投資資本の大きさ、すなわちk3*Cに比例することになる。資本の資源生産への流れに対するR’の比は正味のエネルギー生産(EROI)を表しており、それはk1*Rに等しいことに注意されたい。また、koは資源の資本への変換効率を規定する因子でることに注意しよう。それは技術的な効率に関係するように思われる。ただし、これらの点についてはここでは詳細に調べられない。
システムダイナミクス用のVensim(TM)を使って実行されたモデルは下の通りである。ksは明示的な名称が与えられている。私はまた「脳に優しいモデル」での取り決めを用いて、高い自由エネルギーのストックを低い自由エネルギーのストックの上方に書き表している。
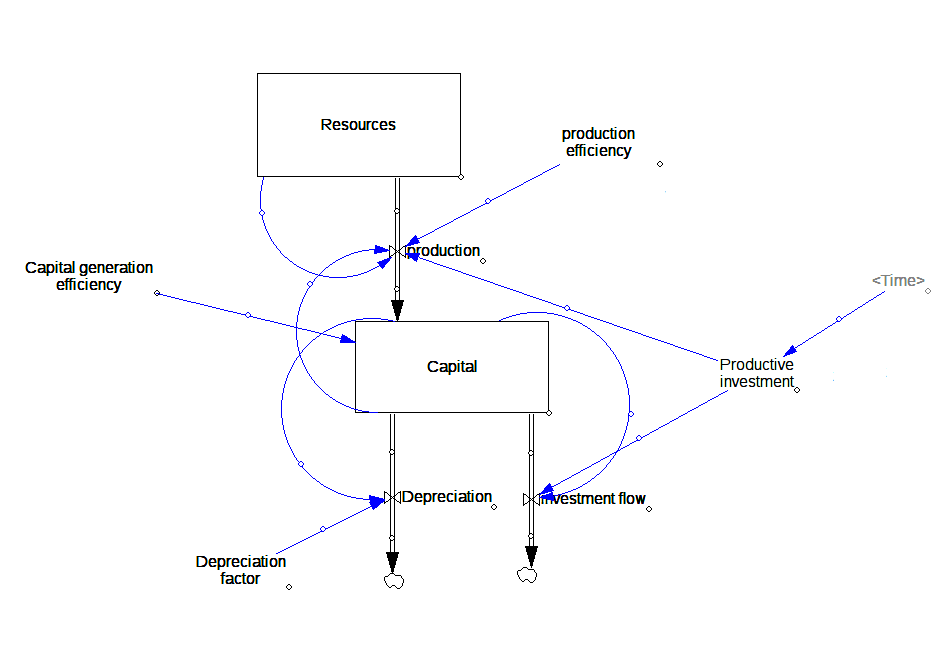
もしksが生産サイクルの間中一定ならば、このモデルで生じる曲線の形状は単純化されたモデルと正確に同じであり、対称的なベル型の生産曲線となる。その典型的な実行結果を示す。
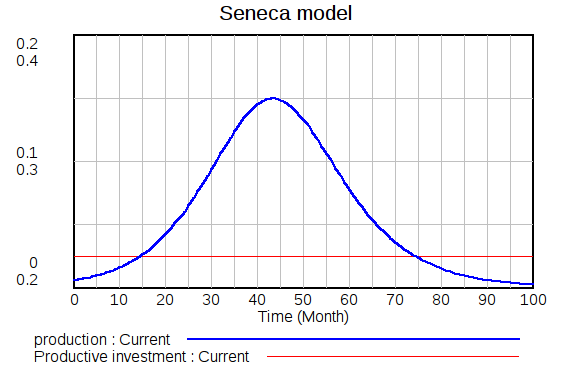
だが、シミュレーション・サイクルにおいてk3の値を変化させるならば、事態は変わる。このモデルの他のパラメータとk3(生産向けの投資割合)を画している特徴は、k3が完全に人為的なものであるということだ。つまり、他のksは物理的要因や技術的要因によって制約されるのに対して、利用可能な資本の生産への再投資はほとんど意志によって選択され得るということなのだ(もちろん、利用可能な資本の総量には制限がある!)。
高い価格は生産者に高い利益をもたらし、新たな開発に再投資される割合を増やす傾向へと導く。生産ピークに近い地域では、鯨油やキャビアの過去の事例然り、価格が高くなる傾向があることも知られている。キャビアの場合には、価格上昇はほとんど指数関数的だったが、鯨油の場合はロジスティック曲線のようだった。再投資される資本の割合が価格に比例して変わることを仮定することで、モデル化が試されるかもしれない。再投資されるcapexの割合が指数関数的な増加をするときに得られた結果を示しましょう。
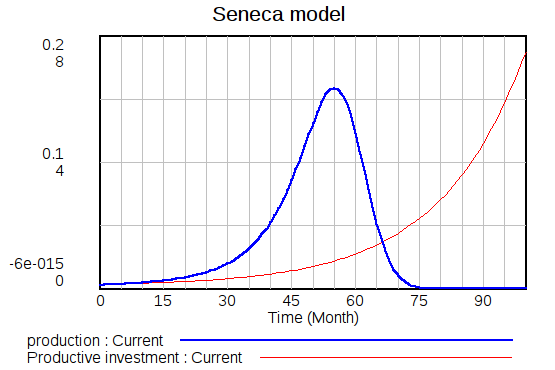
私はまた、k3の上昇傾向を表す別の関数についても調べている。その結果は、線形的な増加でもロジスティック曲線のような増加でも定性的には同じものになる。つまり、再投資されるcapexの割合の増加を仮定する限り、セネカ型の挙動がはっきりと現れるのである。
もう一度強調しておくが、これらは完璧な結果ではない。これらは定数に関する独断的な仮定の下で行われた単なる試験的取り組みである。にもかかわらず、これらの計算結果は、生産者が生産への資本割合を増やしてシステムを延長しようとするときに起こる、一般的な振る舞いがセネカの崖であることを示しているわけだ。



