Ugo Bardi氏の『セネカ効果:衰退局面が成長局面よりも速いワケ』
本稿は、ローマ・クラブおよびASPO(association for the study of peak oil)のメンバーで、フィレンツェ大学地球科学学部の物理化学の教授であるUgo Bardi氏のブログCassandra’s Legacy 2011年8月28 日付けの記事"The Seneca effect: why decline is faster than growth"を訳したものである。
ローマ・クラブの「成長の限界」においても経済ないし文明の成長局面よりも下降(衰退)局面は急峻になると予測されていたが、その現象が「セネカ効果」と命名される。この現象を説明するための”mind-seized”モデルが提示される。「成長の限界」の複雑なモデルに比べて、危機を予期する上で直感的な理解を促す。ここに提示される考え方は教材的価値があるように思われる。
(以下、本文)
「もしもあらゆるものが出来上がるのと同じくらいゆっくりと滅びるのであれば、それは私たちの弱さと私たちの住む世界にとって何らかの慰めとなったことだろう。だが、現実には成長の速度は遅く、破滅に至る時はすみやかだ。」 ルキウス・アンナエウス・セネカ、ルーキーリウスへの手紙、n. 91 (註:大柴芳弘訳『セネカ哲学全集6』(岩波書店)を用いた)
時折、正確になぜなのかは言えないけれども多分に意味ありげに思える何かに出くわすことはないだろうか?長い間私は、物事が悪くなり始めるやますます速く悪化する傾向があるという考えが心に引っかかっていた。私はその傾向を、ルキウス・アンナエウス・セネカが「成長の速度は遅く、破滅に至る時はすみやかだ」と記していたことに因んで、「セネカ効果」あるいは「セネカの崖」と呼びたい。
セネカの崖は私たちがまさに今直面している当のことではないか?そうだとしたら、大変なことだ。石油生産はピークにあるか間もなくピークに向かうとして、経済の緩やかな下り坂を臨むことになると考えることが難しくなるからだ。むしろ、私たちは急速な衰退を目の当たりにするかもしれず、私たちはその状況を「崩壊」と呼ぶことができるだけだろう。その兆候は至る所にあるが、それをいかに証明するか、本当に私たちに降り掛かろうとしていることは何なのか?2000年前に生きていた古代ローマの哲学者の言葉を引用するだけでは十分ではない。私たちはどのような要因が成長局面よりもはるかに速い凋落に私たちを導くのかを理解する必要がある。そのために、モデルを作って、経済システムの様々な要素が崩壊を生じさせるためにどのように互いに連関しているかを調べる必要がある。
私はしばらくこのような考えを巡らせ、今ではモデルを作ることができると思っている。この投稿の残りで扱う内容はそのことについてなのだ。私たちは、これまで営んできたように歩み続けるならば(おそらくそうするだろう)、セネカの崖が実際に私たちの未来だと考えるようになるだろう。ともあれ、詳細にみてみよう。
成長と衰退のモデル
成長と衰退のモデルのお手本はハバート・モデルだ。1956年にマリオン・キング・ハバートによって公表された論文の中に初めて登場したモデルが下掲のもので、彼はアメリカの下部48州の原油生産についての予測を示した。
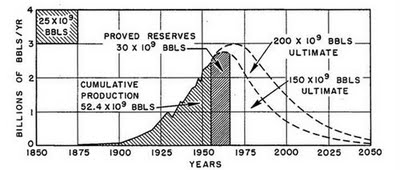
もしあなたがこの話題に関心があるならば、あなたはおそらくこのグラフを何度も見ているだろうし、それが予言としてとても良く当たったことも知っているはずだ。アメリカの石油生産は、ハバートが予言した時期つまり1970年にぴったりピークに達した。ハバート・モデルは、たとえばアダム・ブランドが彼の2007年の論文"Testing Hubbert"に報告しているように、石油生産地域についての多くの過去の事例の良い説明になることが示されている。それは石油だけでなく他の鉱物資源や鯨のようなゆっくりと再生される生物資源(Bardi 2007)についても適用される。
そのようなわけで、私たちは再生不可能な資源の開発にもとづく経済システムの説明のために手始めにハバート・モデルを採用することができる。このモデルの基礎となっている考えは、最も上質で最も高い利益を生む資源から開発が始まるというものである。そして、資源の減耗は徐々に産業がより低い利益の資源開発に移ることを余儀なくする。利益は落ち込み、新しい採掘に投資する産業界の能力も結果として低下する。これが成長を低下させ、ついには、生産活動の衰退を導く(Bardi et al. 2010)。そして、それは地域だけではなく文明全体を説明し得るまさに一般的なモデルなのである。過去に存在した農業文明のほとんどは減耗する資源と肥えた土壌にもとづいたものであり、2009年の私の投稿でも論じた。
しかしながら、ハバート・モデルはセネカ効果を引き起こさないのである。生産を表す曲線の形状が対称的であることが標準的に仮定されているだけでなく、「反セネカ効果」と呼び得る後ろに引けたような曲線形状のいくつかの過去の事例がある。石油生産においてこのような事例があることで、ブランド(2007)は次のように述べている。「減耗速度は成長速度よりも一般に急になるという単純な証拠は過去のデータに認められない。このことは、在来型石油からその代替物への転換に付随してすでに懸念されていることに加えて、生産の急減がさらなる混乱を導くことになると心配する人々には慰めになるニュースであるはずだ。」
結構な話だが、問題があるのだ。ブランドによって報告された結果はすべて地域限定の事例であり、そうでなければあり得ないことなのだ。地域限定の事例においては、採掘コストが跳ね上がったとき、技師たちは単純にコストが安くなる場所に移る。では、移るべき新しい場所がないときにはどうなるか?つまり、世界全体の趨勢を吟味するならばどうなるか?ハバート・モデルにおいて暗黙に仮定されているように、人々は単純に採掘を諦めるのだろうか、あるいは人々はより困難なことに挑戦するのだろうか?はてな、後者の場合には、何が起こるのだろうか?
もちろん、私たちは世界中の一連の石油生産全体に関する過去のデータを持っていない。だが、ハバート・モデルよりもさらに洗練されたモデルがあり、それは私たちに世界全体の趨勢について語り得る。その一つが「成長の限界」の研究で用いられたワールド3モデルであり、1972年にその初版が出版された。そのモデルはハバート・モデルの条件と大きくは異ならない仮定にもとづいているが(2つのモデルを比較した私の投稿を参照のこと)、ワールド3モデルは全体として世界経済について考えている。次に示すのは、2004年のバージョンにおける「標準計算」シナリオの結果だ。
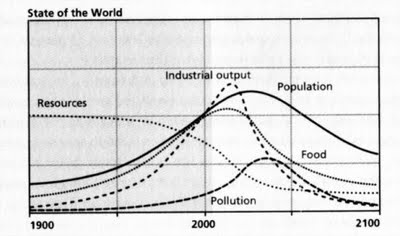
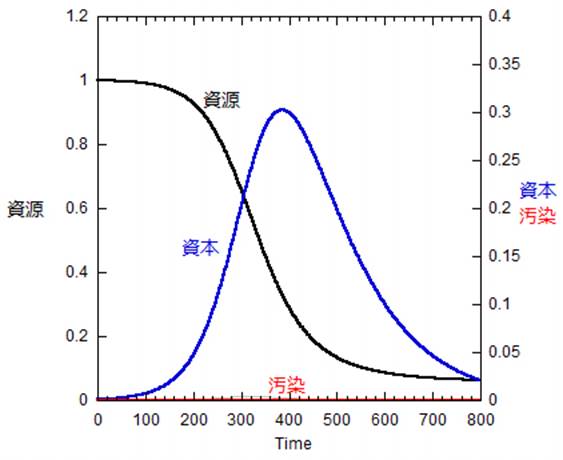
ここで、明らかに食糧生産および工業生産を表す曲線は前のめりになってることを私たちは確認する。それがセネカ効果なのであり、こういったモデルの一般的傾向として現れるものである。この傾向のより明瞭なものは、「成長の限界」の2004年版の表紙に用いられたグラフである。
では、ハバート・モデルのような単純なモデルにはなくてワールド3のような複雑なモデルに現れるセネカ効果を引き起こしている要素は何なのか?この点を理解するために、私は単純な(「脳に優しい」)世界モデルを構築し、どのようなパラメータが前のめりの曲線の原因になるのかを調べてみよう。この曲線形状の非対称性は私たちが「汚染」と呼んでいる要因によって主として導かれることがわかるだろう。
脳に優しい世界モデルの構築 (註:”mind seized”の訳を「脳に優しい」とする)
「脳に優しい」という言い回しは、セイモア・ペーパートの著書"Mind Storms" (1980)の中でつくられた。その著書の見解は、ある現象が真実であることあるいは実際に起こるかもしれないことを確信させるためには、そのことを本当だと思わせねばならないことをあなたは理解する必要がある、というものだ。そのためには、あなたの頭の中で意味付けできるくらいにモデルは十分にシンプルでなければならない。これは1972年の「成長の限界」の研究に伴った問題の一つだった。モデルが複雑過ぎたために、人々は研究の成果を信じなくなるきらいがあったのだ。なぜならば、私が自著で論じたように、人々はモデルがどのように作動しているのかを理解していなかった。そこで、モデルと熱力学との明確な関係性に努めつつ、脳に優しいモデルを作ることができないか、考えてみよう。これは、今年スペインで私が行った講演「エントロピー、ピークオイル、そしてストア哲学」の要旨である。
こういうモデルを構築するために、「成長の限界」の研究に用いられたのと同じ方法である「システムダイナミクス」を用いる。それは、「バルブ」によって調節された「流れ」によって互いに関連付けられる「ストック」のように構成されるものとしてシステムを記述するシミュレーション方法である。システムのこの類の典型は浴槽である。浴槽はストックなのだ。あなたは水の流れによってそれを満たすことができる。あるいは、浴槽から水を出す流れによって空にもできる。このことは「浴槽動力学」と呼ばれ、あなたはリンダ・スウィーニーとジョン・スターマンによるこの主題の素晴らしい論文を読むことができる。浴槽が物理法則に従わなければならないと頑なに主張する必要はないが、時々気に留めて欲しい。ともあれ、浴槽がどのように満たされるのか、また、流れ出るのかを理解するためには、あなたは質量が保存されることを思い出さねばならない。より一般化して言えば、エネルギーは保存されねばならないのだ。これこそ熱力学の第一法則である。あなたはまた熱力学の第二法則も思い出さねばならない。自発的に起こるすべての現象はエントロピーを増大させる、というものだ。つまるところ、浴槽の排水口から水が流れ出すという出来事は、宇宙のエントロピーを増大させている。
それでは、経済システムが再生不可能な資源をどのように開発するかを説明する脳に優しいモデルをつくりましょう。まず、「資源」と呼ぶストックがある。エネルギーは他の資源(たとえば、金属)に変換され得るという考えにもとづくエネルギーのストックであり、そのプロセスは可逆ではないことを仮定する。資源はたとえば「原油」であり、それは文明が依拠する主要な資源だ。そして、「資本」と呼ぶもう一つの箱があり、それは利用可能な形態で蓄えられたエネルギーを表す。このストックは経済の部門であるとも言い得る。つまり、「石油産業」あるいは文明全体を表している。私たちは、熱力学の第二法則が命じるままに、資源ストックから資本ストック、さらには低温の熱の散逸までのエネルギーの流れを描く。これが、そのモデルだ。
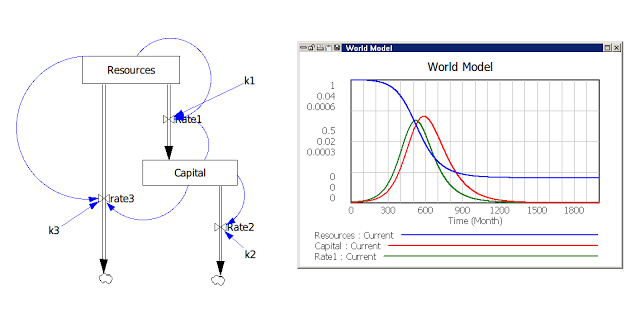
これは私が以前の投稿で示したモデルと同じものだが、エネルギーが高い熱力学ポテンシャルから低い熱力学ポテンシャルに「劣化」する事実を強調するために、以前用いた図を90度右回りに向きを変えた。ちょうど水が浴槽や泉で流れるように。だが、泉や浴槽の場合と違い、ここでの流れはフィードバックによって制御される。つまり資源は、資源と資本の両方の量に比例して、資本に変換されることになる。また、資源は一部、何ら生産に結びつくことなく崩壊することに注意されたい(Rate3)。これは生産過程の非効率性による。石油が漏れたり、天然ガスがベントされて燃やされたりしていることを想像して欲しい。
確認できるように、生産を表す曲線(図中のRate1)はベル型で左右に対称的な形状である。このモデルは実質的にハバート・モデルに等しい。問題は、3つの定数の値を変えてあなたはこのモデルを好きなだけ試すことができるものの、曲線はセネカ効果を現さない、つまり、崩壊が成長よりも速くならない、ということなのだ。はてな、私たちは何を忘れているのだろうか?
実を言えば、私たちは「成長の限界」の研究に用いられた世界モデルに含まれる、ある要素を忘れている。私たちが忘れているものは汚染であり、あるいは、もっとうまく言えば、汚染の影響だ。上述の単純なモデルでは、劣化したエネルギーは無害なまま宇宙に散逸している。つまり、モデルの他の要素に影響を及ぼしていないということになる。だが、私たちが知っているように、現実の世界では、このことは事実ではない。汚染はコストである。お金と資源が汚染と闘うために費やされねばならない。それは水質汚染や大気汚染であり、地球温暖化のような影響を及ぼす。
汚染の影響をシミュレートするために、それを3つ目のストックとして定義する。それは資本ストック(註:下図では”Economy”と表記されている)から資本ストックと汚染ストックの両方の大きさに比例してエネルギーを流し出す(註:Rate2)。なお、いくつか定数があるので、私は損失lossに因んで「l」という記号を使ってまとめている。これら(l1, l2, l3)は直接ストックから外の空間に出て行く流れに関係している。これがモデルだ。私はセネカ効果を強調するようなパラメータを選んで、そのサンプルとなる結果を示している。
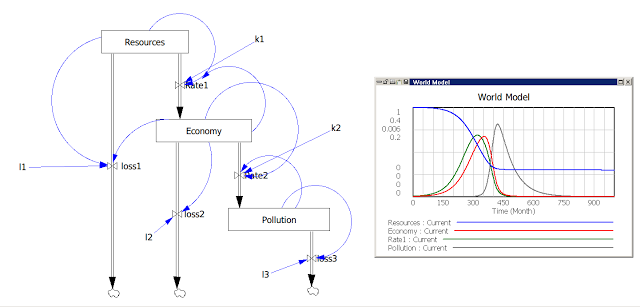
この計算のパラメータはk1=0.03. k2=0.3, l1=0, l2=0.01, l3=0.015, 初期値として資源Resources (t0)=1, 資本Capital(t0) =0.001, 汚染Pollution(t0)=0.001 を用いた。
これは別の計算からのもので、生産を表す曲線を単独で示している。
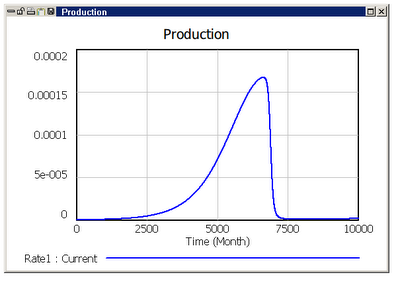
このモデルは、「セネカの崖」を明示する「セネカ的」な生産曲線を与え得るのだ。その曲線はゆっくりと上昇し、その後急速に崩壊する。セネカが言うように、「破滅に至る時はすみやかだ」。 ようやく私たちは何がセネカの崖を生じさせるのかを言葉にすることができるのだろうか。その通りだ。それはこのようなものだ。まず、汚染の影響は経済的資本を抜き取るようなことだと考えていただきたい。次いで、汚染ストックは経済ストックを育むことに伴って成長してしまう。つまり、汚染はそれが大きくなる前に経済が成長することを待たねばならない、と考えていただきたい。プロセスが進むにつれて、経済から漏れ出すエネルギーの速度が大きくなることを導くのはこの遅れなのだ。経済ストックの大きさが生産速度を決定するので、私たちはピークの後になって急激にパラメータが速く小さくなるのを看取することになる。これこそセネカ効果の本質である。
では、このモデルのもっと深いところを探ってみよう。多くのトラブルを招くこの「汚染」とは正確には何のことだろうか?それは、宇宙空間に無害なまま消えていく赤外線放射とは違う何かを示すために「成長の限界」の著者らが「残留性汚染」と呼んだ当のものなのだ。それはとても一般的な概念であり、資本によって作り出され、資本から資源を抜き取る要素を含んでいる。たとえばフクシマの惨事は、それを作り出した産業に痛手となって戻ってくる汚染の好例である。大気や水の汚染もそうだ。地球温暖化や戦争もそうだ。戦争は汚染の大きな作り手だし、核戦争はセネカ効果をほとんど直ちに引き起こすだろう。
このモデルがどのように振る舞うかを理解する今、私たちはブランドの研究に戻って、石油生産に関する過去の研究例の多くが対称的な推移すなわち「反セネカ的」推移を示す理由を説明することができる。私たちはセネカ効果が汚染によって生じると言った。ならば、「反セネカ的」な結果は石油の採掘が汚染を生じないことを意味するのだろうか?もちろん、まったく違う。石油を採掘する人々は彼らが作り出している汚染に注意を払うことを必要としていないことを意味しているだけのことだ。具体例を挙げるならば、アメリカの下部48州からの石油採掘において、残留性汚染は主として環境中に加えられた二酸化炭素や他の温室効果を有するガスのかたちをとってきた。これはまだ私たちに悪影響を及ぼしていないが、いずれ、地球温暖化によるダメージに人々は注意を払わねばならなくなるだろう。その請求書が届くならば、支払えるつもりでいたよりも随分と高い代償であることに気づくかもしれない。
技術の進歩はセネカの崖から私たちを救うだろうか?どうだろう、自ずとそうなりはしないだろう。実際には、崖は思いの外急峻なものになり得るだろう!技術をシミュレートする一つの方法は、上記数学モデルの定数を一定ではなく、技術の進展と共に変化させることを想定することに等しい。 たとえば、定数”k1” の増加する値が資源開発における技術進歩に対応する。それは一連の資源開発の終盤に生産する全量を増加させるが、私の論文の中で論じたように(Bardi 2005)、ピーク後のより険しい落ち込みも生じさせる。より興味深いデータは定数"k2"を徐々に小さくなるように微調整することである。これは汚染の発生を抑える技術の進展を促進することに相当する。言い換えるならば、数学モデルは私たちに「クリーン生産技術」は一連の生産をより対称的な曲線形状に近づけるという意味においてよい考えなのである。
読者はこの数学モデルに、たとえば、もっとストックを加えて複雑性を増すなどの改良を加えるかもしれない。エネルギーを溜め込んで浪費する「官僚制度」ストックはどうだろう?思うに、それは「汚染」ストックと同じように振る舞うだろう。おそらく、官僚制度は汚染の一形態であると言い得るだろう。それはそうと、この加えられたストックによって、利益よりも問題を生み出す複雑性の増加によって文明が衰微崩壊するというテインター・モデルと同様の数学モデルになることを付記しておこう。もしもモデルにさらなるエレメントを加え続けるならば、やがてあなたは「成長の限界」の研究で用いられたワールド3モデルと同様のものを作り出すことになるだろう。そのモデルが前のめりの曲線を描くことは先に言及した通りである。
モデルを改良するには多くの方法があり、セネカ効果が唯一の可能な結果ではない。定数をいじくって、読者は逆の振る舞いを描くことができるかもしれない。つまり、成長よりもゆっくりと減衰する「反セネカ的」曲線だ。読者が期待するように、それは汚染の蓄積を最小化する定数を使って起こる。だが、一般に、セネカ効果は、この類のモデルにおける「堅固な」性質なのであり、様々な仮定のために出てくる。読者は自己責任でセネカ効果を知らんぷりするわけだ。
現実世界におけるセネカ効果
セネカ効果の歴史上の実例はあるだろうか?いくつかあるにはあるのだが、私たちは定量的なデータについては多くを持ち合わせていない。たとえば、古代ローマの文明はピークに達するまでにおよそ7世紀、そして、西ローマ帝国の没落までにおよそ3世紀かかった。(セネカ自身、彼の存命中にローマの衰退に気づいていたかもしれない。)しかしながら、ローマ帝国の人口のようなパラメータとして残っているデータは、前のめりの曲線に表れる効果を調べるには十分によいものではない。
代わりに、マヤ文明に相応しいデータがある。ダニングら(1998)の研究からの画像を下に示す。横軸はとても長く、洪積世/完新世の境界から10000年になる。
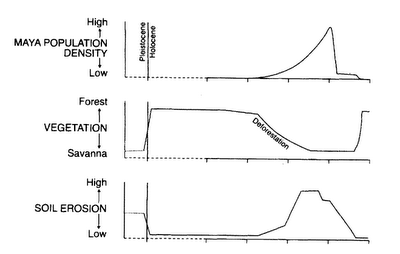
この場合、汚染とは、資本となる資源を流出させて人口の崩壊を引き起こす、土壌の浸食のことである。この説明には注意を要する。なぜならば、幾人かの研究者はマヤ文明の崩壊は気候変動によって導かれたと信じているからだ。だが、本稿で展開した世界モデルは歴史データと合致しているように思われる。
もっと私たちに馴染み深いものでは、ディミトリー・オルロフの論文 "Peak oil is history"(邦訳「ピークオイルはすでに歴史だ」)で使われた図がある。それはロシアの石油生産を表している。
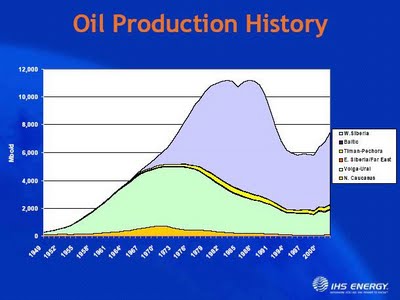
ソ連は、崩壊前にはほぼ閉鎖された経済であり、「小世界」を形成していた。ロシアの石油生産がピーク後いかに急速に減じたか、つまり見事なセネカの崖の様相を呈していたことに気づいていただきたい。そしてまた、後から生産がどんなふうに再び回復したか、気に留めていただきたい。ある時点でソ連は、孤立した経済システムとして存在することを止めて、全世界の経済システムの一員になったのだ。その時点で、私たちが用いた単純なモデルは適合しなくなっている。なぜならば、資本ストックがモデルの外側からの資源の流入を受け入れたためである。
結論:杯盤狼藉
とてもしばしば、私たちは行動の遅延効果を理解することに失敗する。このことをジョン・スターマンは地球温暖化についての講演の中でロバート・ルイス・スティーブンソンの言葉を引用して思い出させてくれている。それは「誰もが遅かれ早かれ杯盤狼藉の席についている」というものだ。本稿に示した数学モデルは、セネカ効果は遅延した成り行きの結果だと私たちに教えている。
いつものように、未来は私たちの行動で築かれる当のものだが、モデルはどのような行動がゆくゆくある結果に私たちを導くかを教えてくれるだけだ。このように用いるならば、モデルはとても有益であり、モデルは文明全体を扱うよりも、たとえば、一企業や人間関係といったはるかにより小さなシステムに適用可能なものになる。いずれにせよ、セネカ効果は常態を保とうとすることが困難になることの結果であろう。そうして、物理的な意味の資源だろうと信用の蓄えだろうと、私たちはシステムを稼働し続けるための資源を速く失うことになるのかもしれない。この成り行きを避ける方法は、システムに私たちの望みを無理強いするのではなく、システムが欲する経路にシステムを委ねることである。言い換えるならば、おそらくセネカ自身が言ったように、ある種の禁欲的な生活の中に物事を捉える必要がある。
世界中の状況と関連する問題、地球温暖化や資源の減耗について考えるならば、モデルが私たちに教えてくれることは、セネカの崖はすでに減耗している天然資源にたよりすぎることの避けられない結果なのかもしれない。代わりに、私たちは再生可能(あるいは原子力)エネルギーのような代替資源の貯蔵を進めるべきなのだ。同時に、私たちはタールサンド、オイルシェール、深海油田のような汚染源ともなり高価でもある資源の開発を避けるべきであり、また、一般に、"drill, baby, drill"哲学(註:2008年の共和党のスローガン)の適用も避けるべきだ。残念ながら、こういった避けるべきことがまさに私たちが取り組んでいることの例なのだが。
セネカは、友人のルーキーリウスへの手紙の中で彼が著した考えを実践しようとして私たちが取り組んでいる惑星規模の出来事を考えていたのかどうか、彼が言ったことを私は知らない。私はただセネカがある種の禁欲をもって出来事を観ていたと想像できる。あるいは、おそらくセネカは彼の「摂理について」で述べたことをコメントすることだろう。「われわれはそうなるべく用意されているのだ。自然は望むように己の身体を用いるがよい。われわれは、いっさいの出来事に対して、喜びのうち雄々しくこう考えようではないか。――われわれに属するものは何も滅びない、と。」(註:セネカ著 兼利琢也訳『怒りについて 他二篇』岩波文庫による)
ディミトリー・オルロフが書いた記事"Peak Oil is History”(邦訳「ピークオイルはすでに歴史だ」)からこの投稿のインスピレーションの源を得たことを彼に感謝したい。
___________________________________________
参考文献
Bardi, U., 2007, Energy prices and resource depletion: Lessons from the case of whaling in the nineteenth century” Bardi U. Energy Sources, part B- Economics Planning and Policy Volume: 2 Issue: 3 Pages: 297-304
Bardi, U. and Lavacchi, A., 2009, "A Simple Interpretation of Hubbert’s Model of Resource Exploitation” Energies 2009, 2(3), 646-661; doi:10.3390/en20300646
Bardi, U. 2011 "The Limits to Growth Revisited", Springer, ISBN 978-1-4419-9415-8
Bardi, U., Lavacchi, A., Yaxley L., 2011 “Modelling EROEI and net energy in the exploitation of non renewable resources” Ecological Modelling, In Press.
Brandt, A.R. (2007). Testing Hubbert. Energy Policy, 35(May):3074-3088. DOI: 10.1016/j.enpol.2006.11.004
Dunning, N., D. Rue, T. Beach, A. Covich, A. Traverse, 1998, "Human – Environment Interactions in a Tropical Watershed: the Paleoecology of Laguna Tamarindito, Guatemala," Journal of Field Archaeology 25 (1998):139-151.
<訳者による補記>
『成長の限界』の予測を振り翳すことは、「如是我聞」やら「主はこう言った」という根拠だけで教典を吹聴する権威主義的な営みに似ている。人々に石油文明の危機を得心してもらうには、工夫が肝要である。
『成長の限界』レポートの著者だったドネラ.H.メドウズらの著書” BEYOND THE LIMITS: Confronting Global Collapse, Envisioning a Sustainable Future”(邦訳『限界を超えて 生きるための選択』)には、「ワールド3を用いた研究と教育のために」と題する付章があり、ワールド3によるシミュレーションを要素ごとに理解するための説明が記されている。だが、それは、端的に言って、とても理解しようという気になれない代物である。過ぎたるは猶及ばざるが如し、まさにジョセフ・テインターの見返りに乏しい複雑性が崩壊を導くという論を想起させるほどの複雑さである。対して、バルディ教授の取り組みは、まさにオッカムの剃刀である。
だが、残念ながら、日本の教育現場において「システムダイナミクス」は馴染み深い手法ではない。幸い、本稿で示されたモデルは微分方程式として明示してもさほどの行数を要さないくらいに脳に優しい。高校3年生レベルの微分・積分に幾ばくかの学習を加えれば、人々は自らセネカ効果を確信して、世界の行く末を思索する糧にできるはずだ。以下にその考え方を記す。 資源をR、資本をC、汚染をPとすると、本文で示されたモデルは次の微分方程式で表される。
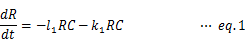
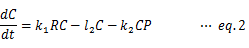
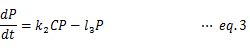
たとえば、eq.1を時間の関数として明示的かつ離散的に表記すると、次のようになる。
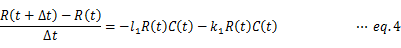
R(t+Δt)について解けば、
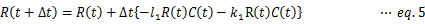
かくして、定数l1、k1、初期値R(0)、C(0)、計算間隔Δtの値が与えられれば、R(Δt)の値が算出可能である。同様に、eq.2からはC(t+Δt)、eq.3からはP(t+Δt)についての漸化式がそれぞれ求められる。定数とR(Δt)、C(Δt)、P(Δt)の値からR(2Δt)、C(2Δt)、P(2Δt)の値が求まり、定数とR(2Δt)、C(2Δt)、P(2Δt)の値からR(3Δt)、C(3Δt)、P(3Δt)の値が求まる。このような計算を繰り返して、シミュレーション結果が得られる。表計算ソフトexcelを用いて計算した結果の例を以下に示す。
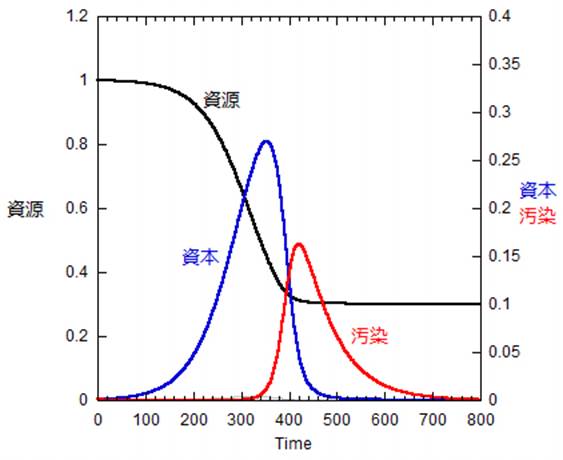
k1=0.03. k2=0.3, l1=0, l2=0.01, l3=0.015, 資源R (0)=1, 資本C(0) =0.001, 汚染P (0)=0.001 としてExcelで計算した結果。セネカ効果を確認できる。
「汚染」のない場合(P(t)=0)の計算結果は以下の通りであり、セネカ効果が現れない。